[백준] 9475. 파스칼 제곱

문제

파스칼 행렬은 크기가 무한대이며 다음과 같이 정의한다. (행과 열 번호는 0부터 시작한다)

Pascal[row, column] = Comb(row, column) for 0 ≤ column ≤ row

위의 경우를 제외한 곳은 모두 0이다. Comb(n, k)는 조합이다.

1	0	0	0	0	0	0	0	0	0	...
1	1	0	0	0	0	0	0	0	0	...
1	2	1	0	0	0	0	0	0	0	...
1	3	3	1	0	0	0	0	0	0	...
1	4	6	4	1	0	0	0	0	0	...
1	5	10	10	5	1	0	0	0	0	...
1	6	15	20	15	6	1	0	0	0	...
1	7	21	35	35	21	7	1	0	0	...
1	8	28	56	70	56	28	8	1	0	...
1	9	36	84	126	126	84	36	9	1	...
.	.	.	.	.	.	.	.	.	.	.
.	.	.	.	.	.	.	.	.	.	.
.	.	.	.	.	.	.	.	.	.	.

파스칼 행렬의 제곱을 구하는 프로그램을 작성하시오.

PascalP = Pascal × Pascal × ... × Pascal

---

입력

첫째 줄에 테스트 케이스의 개수 K (1 ≤ K ≤ 1000)가 주어진다.

각 테스트 케이스는 네 정수로 이루어져 있다. 첫 번째 정수는 테스트 케이스 번호이다. 두 번째 정수는 P이다. (1 ≤ P ≤ 100,000) 세 번째 정수와 네 번째 정수는 R과 C이다. (0 ≤ C ≤ R ≤ 100,000)

출력

각 테스트 케이스마다 테스트 케이스 번호를 출력하고, PascalP의 R행 C열의 값을 출력한다. 답이 64비트 정수 범위를 넘어가지 않는 입력만 주어진다.

---

답이 unsigned 64bit 정수이기 때문에 long형으로 접근이 불가능하다. 결과는 무조건 양의 정수이기 때문에 Java를 기준으 로 long의 범위를 넘어서는 BigInteger를 사용하였다. 이거 해결한다고 시간이 꽤나 오래걸렸다.

R과 C의 범위가 10만, 제곱수의 범위도 10만이기 때문에 N, R의 Combination을 구할 때 최적화가 필요하다. 필요없는 부분은 계산을 하면 안된다.

 

행렬의 제곱을 구할 땐 분할정복을 이용한다. 행렬 제곱을 2~3번 해보면 규칙이 생긴다.

 

nCr을 구한 값에 P를 n-r번 제곱한 값을 곱해주면 된다.

 

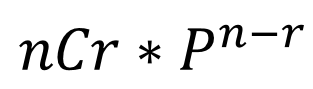
먼저 P의 n-r제곱을 구하는 분할 정복 부분이다. 이 부분은 기본 개념이랑 크게 벗어나지 않는다.

public static long dnq(long k, int pow) {
    if(pow == 1) {
        return k;
    } else if(pow == 0) {
        return 1;
    }

    long res = dnq(k, pow / 2);

    if(pow % 2 == 1) {
        return res * res * k;
    } else {
        return res * res;
    }
}

홀수일 경우와 짝수일 경우를 구분해주는 것이 포인트이다.

 

nCr을 구하는데 최종 값이 long형을 벗어날 수 있기 때문에 자료형을 통일하기 위해 BigInteger를 사용하였다.

※ BigInteger는 객체를 생성할때 파라미터로 String형태를 받는다.

public static BigInteger comb(int n, int r) {
    if(r < 0 || r > n) {
        return BigInteger.ZERO;
    }
    if(r == 0 || r == n) {
        return BigInteger.ONE;
    }
    BigInteger dn = new BigInteger(String.valueOf(n));
    BigInteger dk = BigInteger.ONE;
    if(r > (n / 2)) {
        r = n - r;
    }
    BigInteger res = BigInteger.ONE;
    for(int i = 1; i <= r; i++) {
        res = res.multiply(dn).divide(dk);
        dn = dn.subtract(BigInteger.ONE);
        dk = dk.add(BigInteger.ONE);
    }

    return res;
}

조합의 특성을 이용하여 r이 0보다 작거나 n보다 클경우는 경우의 수가 없으니 BigInteger.ZERO를 리턴

r이 0이거나 r와 n이 동일할 때 경우의 수는 1이니 BigInteger.ONE을 리턴

 

최종값을 계산하기 위해 n과 1부터 시작할 k를 BigInteger형으로 다시 만들어 준다.

 

여기서 최적화를 한번 해야되는데 조합의 특성을 잘 보면 절반을 중심으로 좌/우가 대칭이다.

 

1

7

21

35

35

21

7

1

0

0

계산을 끝까지 할 필요 없이 r이 n/2가 넘어가버리면 n에서 r만큼 뺀 상태와 구하는 값이 똑같기 때문이다.

if(r > (n / 2)) {
    r = n - r;
}

 그리고 r값을 최적화를 했다면 나머지는 조합을 구하는 방법을 그대로 적용한다.

BigInteger res = BigInteger.ONE;
for(int i = 1; i <= r; i++) {
    res = res.multiply(dn).divide(dk);
    dn = dn.subtract(BigInteger.ONE);
    dk = dk.add(BigInteger.ONE);
}
return res;

 

---

import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.math.BigInteger;
import java.util.StringTokenizer;

public class Main9475 {
    public static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    public static BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
    public static void main(String[] args) throws Exception {
        int K = Integer.parseInt(br.readLine());
        StringBuilder sb = new StringBuilder();
        for(int k = 0; k < K; k++) {
            StringTokenizer st = new StringTokenizer(br.readLine());
            int tc = Integer.parseInt(st.nextToken());
            int P = Integer.parseInt(st.nextToken());
            int n = Integer.parseInt(st.nextToken());
            int r = Integer.parseInt(st.nextToken());
            BigInteger res = comb(n, r);
            BigInteger l = new BigInteger(String.valueOf(dnq(P, (n - r))));
            sb.append(tc).append(" ").append(res.multiply(l)).append("\n");
        }
        bw.write(sb.toString());
        br.close();
        bw.flush();
        bw.close();
    }

    public static BigInteger comb(int n, int r) {
        if(r < 0 || r > n) {
            return BigInteger.ZERO;
        }
        if(r == 0 || r == n) {
            return BigInteger.ONE;
        }
        BigInteger dn = new BigInteger(String.valueOf(n));
        BigInteger dk = BigInteger.ONE;
        if(r > (n / 2)) {
            r = n - r;
        }
        BigInteger res = BigInteger.ONE;
        for(int i = 1; i <= r; i++) {
            res = res.multiply(dn).divide(dk);
            dn = dn.subtract(BigInteger.ONE);
            dk = dk.add(BigInteger.ONE);
        }

        return res;
    }

    public static long dnq(long k, int pow) {
        if(pow == 1) {
            return k;
        } else if(pow == 0) {
            return 1;
        }

        long res = dnq(k, pow / 2);

        if(pow % 2 == 1) {
            return res * res * k;
        } else {
            return res * res;
        }
    }
}